IRIS on a Torus: Growing Convex Sets on Manifolds

My current research focus at MIT is motion planning along manifolds, which we're primarily exploring through the lens of the graph of convex sets framework, abbreviated as GCS. (Refer to a previous blog post for more details, or check out the papers of Marcucci et. al. here and here.) Convexity is a property that is examined through the lens of Euclidean geometry, but it is possible to consider it in the broader context of smooth manifolds. This is reliant on the idea of a geodesic: a shortest path on a manifold.

Replacing Euclidean spaces with manifolds and lines with geodesics allows us to consider a graph of geodesically convex sets (GGCS). We've begun laying the groundwork for planning over manifolds with such a tool, and you can read about it in our paper Non-Euclidean Motion Planning with Graphs of Geodesically-Convex Sets, to appear at RSS 2023. (You can read the preprint today on arXiv!)

While GGCS assumes the geodesically convex sets are given, computing such sets is an important part of the framework. GCS is best friends with the IRIS algorithm, which can produce collision-free convex sets. (I discussed IRIS in another previous blog post, and you can read the original paper here.) It turns out that just as convexity can be easily generalized to manifolds, so too can IRIS. In particular, we use IRIS-NP, which can handle the nontrivial kinematic mappings between configuration space (where we plan) and task space (where the obstacles live).

Before I can describe how we modified IRIS-NP to work on manifolds, I'll provide some brief theoretical background. A manifold is a locally Euclidean space, generalizing the idea of smooth curves and surfaces to arbitrary dimensions. A Riemannian metric is an additional piece of structure we can put on a manifold that, among other myriad things, allows us to measure the length of a path. A curve is called a geodesic if any small enough segment of it is length minimizing. For example, geodesics in Euclidean space are lines, and geodesics on the sphere are great circles.

Geodesics allow us to generalize convexity to manifolds. A set S is geodesically convex (henceforth abbreviated g-convex) if for every pair of points x and y in S, there is a unique length-minimizing geodesic connecting them, and it is entirely contained in S. This definition is somewhat more verbose than the definition of ordinary convexity, due to the non-uniqueness of geodesics. For example, for any two points on the sphere, the great circle connecting them describes two possible geodesics. And there are infinitely many shortest paths between the north and south pole of a sphere.

With the preliminaries out of the way, we can now discuss the modifications to IRIS-NP. Given a seed point on the manifold, we consider a maximal coordinate chart containing it. (In particular, we consider the Riemannian normal coordinates, up to the cut locus.) We then try to grow the region under the image of this chart, in effect, growing the polytope in a full dimensional space. The inverse of the chart mapping is simply precomposed with the forward kinematics function when checking collisions. In other words, to check if a point in the image of the chart is collision free, we lift it to the manifold, and then apply forward kinematics.

Because IRIS-NP is leveraging nonlinear programming, this doesn't lead to many programmatic changes. However, there is a more subtle problem: the minimizing geodesic can go "the wrong way around" the manifold. This means that sets which look convex in the coordinate chart may not be g-convex when lifted to the manifold! In the case of the sphere, the northern hemisphere (up to, but not including the equator) is g-convex. But if the set is extended to include any of the southern hemisphere, then g-convexity is lost, even though the set still looks convex in the chart's coordinate system.

For any point on a Riemannian manifold, there is a strictly positive "radius of convexity" about that point. For any ball with radius less than this quantity, the ball is g-convex. If the manifold is compact, we can consider the minimum convexity radius -- so any ball on the manifold with radius smaller than that quantity will be g-convex. This enables us to grow g-convex sets on a chart, while capping its size in such a way as to guarantee the minimizing geodesics can't go the wrong way around. (The details for why this is true can be found in our paper.)

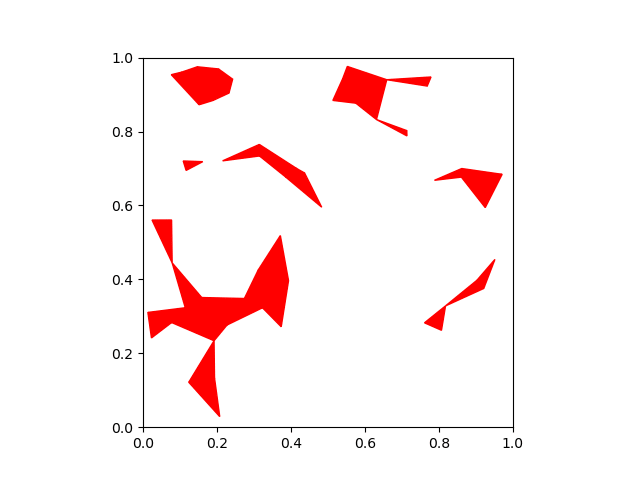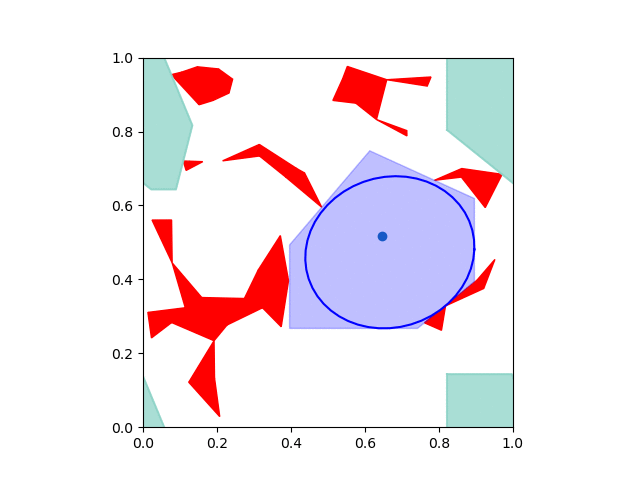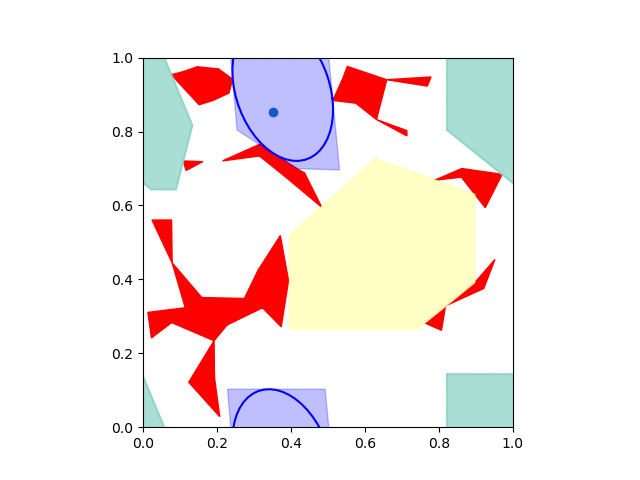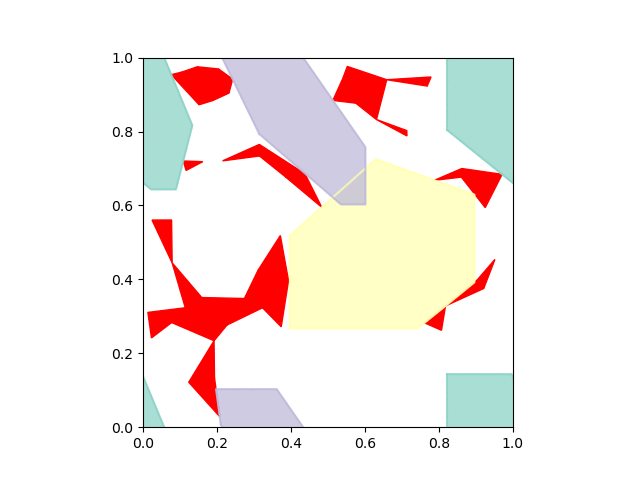
As an illustrative example, consider the torus manifold. (The torus may seem like a contrived example, but it's actually precisely the configuration space of a robot with two continuous revolute joints.) Instead of the classic "donut" picture, we can realize it as a square, with the opposite edges identified:

Making a Torus from a Square

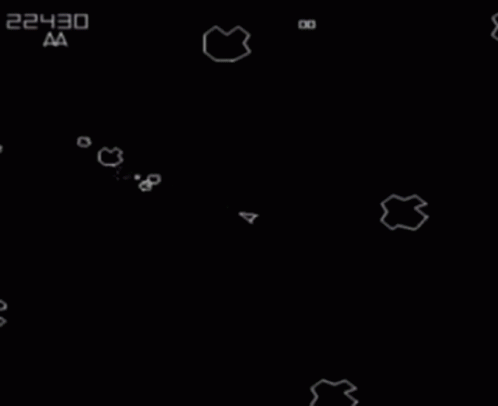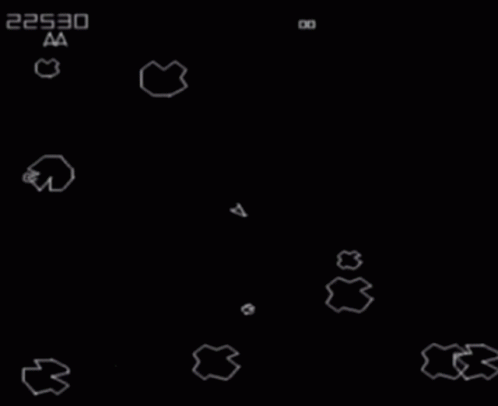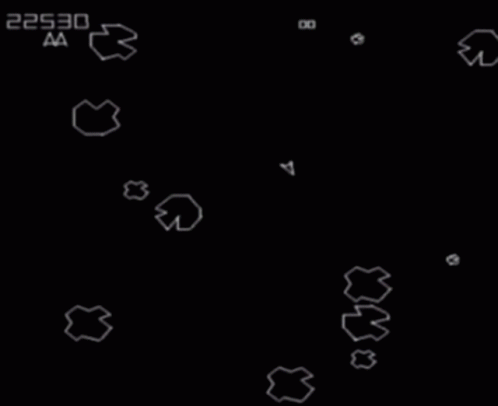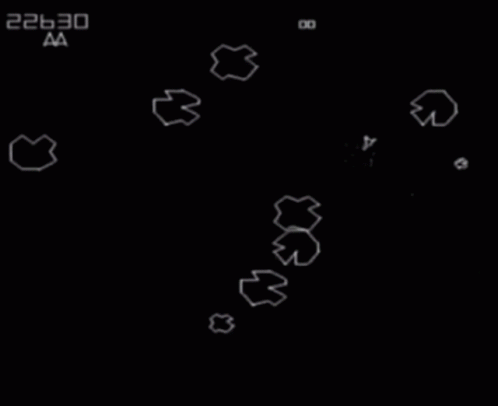
The classic arcade game Asteroids uses this.

Here's what it looks like when you grow IRIS regions on a torus:

Note that we don't need to use IRIS-NP, since the obstacles are convex and have closed-form representations in configuration space. You can play with the code yourself -- just download it from this git repository.