Reimplementing GCS (Shortest Paths in Graphs of Convex Sets)
In a previous blog post, I discussed my experiences reimplementing Iterative Regional Inflation by Semidefinite programming (IRIS), which is an algorithm for finding large convex regions of collision free space (C-Free). In this blog post, I'll be discussing my experiences reimplementing shortest paths in Graphs of Convex Sets (GCS), an algorithm for motion planning when the configuration space is described as the union of convex sets.
Disclaimer: the intent is not to build a codebase for future use, since the Drake toolbox has mature implementations of both IRIS and GCS.
Disclaimer: if you have not read the previous blog post, you should do so before reading this one.
In this blogpost, I'll give a brief overview of the GCS paper, and then discuss my experiences reimplementing it. Before reading this blog post, you should read my previous blog post about reimplementing IRIS, as it provides some background and context which I will not repeat in this post. I have also made my code available on github, with links included at the end of this post.
An Overview of GCS
The shortest path problem is potentially the most well-known problem in all of computer science. In robotic motion planning in particular, it is frequently used as a component of sample-based planners. These planners build up a graph within C-Free, where vertices denote collision-free poses, and edges connect nearby vertices. When it's time to actually compute the path between two points, the problem that must be solved is precisely the shortest path problem.
GCS broadens the motion planning version of the shortest path problem to handle convex regions of C-Free (such as those produced by IRIS), instead of just individual points. As a result, it can plan globally optimal paths. In comparison, sample based planners would require extraordinary many sample points to produce similar results. Trajectory optimizers could potentially produce such paths, but they're very likely to get stuck in local minima, and produce non-optimal paths.
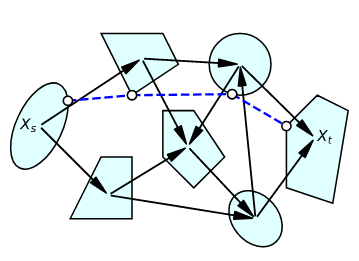 |
| A shortest path problem for GCS. |
GCS allows the shortest path problem to function with convex sets by including the position of the vertices as decision variables, with constraints so that they're contained in their corresponding convex sets. Edge weights are no longer constants, but now depend on the position of the vertices. Using the Euclidean distance as an edge weight is the standard approach, although any convex function can be used. Solving the shortest path problem now require selecting the positions of the vertices, as well as the path across the graph. To solve this problem, GCS is formualted as a formal mathematical optimization problem; specifically, GCS is a mixed-integer convex program.
A mathematical optimization problem is a problem where one is asked to minimize (or maximize) a function over some domain (called the feasible set). Although this domain could be any abstract set, it is often defined in terms of various constraints on the optimization variables. It's difficult to handle every possible optimization problem in complete generality, so one frequently examines specific subclasses. An example subclass is linear programming: the case where the objective function is linear, and the feasible set is described by linear inequalities.
The two properties of GCS' optimization problem that classify it most are its integrality (integer-ness), and its convexity. Convexity is a property of both sets and functions. A set is convex if, for any two points in the set, the line segment connecting them is also contained in the set. A function is convex if, for any two points in its domain, the line segment connecting them in the graph of the function lies above the actual value of the function. Convex optimization problems are well understood, and can quickly be solved to global optimality. Integrality refers to the constraint that an optimization variable be integer-valued. Solving such problems is called integer programming, and it is very hard, both in theory and in practice. (It may take exponential time to solve even very simple problems.) GCS is a mixed integer program, meaning that some of its optimization variables are integers, and others are real-valued.
 |
| The mathematical program formulation of GCS. |
A natural question to ask is, "Why is GCS useful if integer programming is so hard?" There are a few reasons, related to the way that GCS is formulated. For one, the formulation of GCS uses fewer integer variables than similarly-constructed programs, making the problem less complex. Also, the convex relaxation (when the integer variables are allowed to take continuous values) of GCS is often very close to the true optimum.
After solving the convex relaxation, and then computing a final path through the graph with a greedy depth-first search, we have an answer (although we have no idea if it's optimal). However, we can give a bound on how far this answer is from the optimal solution. We know that the convex relaxation is no worse than the true (unknown) optimal solution, and we know that the greedy solution is no better than the true solution. So we can evaluate whether or not the integer program needs to be solved, or at least partially solved further before computing the relaxation again. So although it's possible for GCS to perform poorly for certain problems (indeed, examples are presented in the paper), it's still a valuable tool in practice.
Implementing GCS
For my implementation of GCS, I wanted to handle a very simple case. I set up a basic experiment in a 2D world, where there's a square obstacle, and I want to move from a point from one side of the point to the other. I generate the convex regions with IRIS with fixed initial points (although I can use random points as well). I then determine which IRIS regions overlap, in order to determine the graph structure for GCS.
At this point, there are two equivalent options for formulating GCS. One option is to constrain each line segment in the path to lie within a specific convex set, and then constrain their endpoints to be equal. Another option is to constrain the endpoint of each edge to lie within the intersection between IRIS regions. If using Bezier curves to build up a trajectory instead of line segments, as was done in another paper by the authors of GCS, the former option makes more sense. However, I elected to use the latter formulation, as it has fewer decision variables (and seemed simpler to implement).
One major impact from using the latter approach is that the graph structure changes. Because the intersection sets are now the regions for GCS, the edges and vertices are different. In particular, we have constructed the conjugate graph, where each edge becomes a vertex, and two vertices in the new graph are joined if their edges in the original graph shared an endpoint.
At this point, all that remains to be done is actually implementing the GCS optimization problem. I used CVXPY to implement the convex relaxation (although it can also solve the integer programming version directly). There's not much about this process that's interesting to describe -- although the optimization problem is challenging to implement, it's relatively straightforward.
Whether solving the convex relaxation, solving the integer formulation, or partially solving the integer formulation and solving the relaxation at that point, the final step is computing the output path in the graph using greedy depth-first search. Below is an image of the final path computed in the toy scenario.
 |
| The optimal path, as found by GCS (using the convex relaxation). |
Conclusion
I've published my code for GCS online in this git repository,
so you can download it and try it out for yourself. You can also find my code for IRIS in this git repository.



Hi there! First of all, thanks for creating these blogs, they are very informative and highly appreciated!
ReplyDeleteI came across your name and webpage from this presentation by Russ (https://youtu.be/KSCC7mVJzaw?list=PLCFD85BC79FE703DF&t=3034). I am currently a master's student at KTH (Sweden) and am exploring using the GCS algorithm for motion planning with cartesian path constraints. I think you and the group's work on extending GCS to non-euclidean spaces would be very valuable. Would there be any chance that the progress/results of the work could be shared with me?
Hi Rufus. Sorry for not responding to this sooner -- I hadn't properly configured Blogger to notify me when people comment. (Now fixed, hopefully!) The work Russ mentioned in that talk isn't quite ready for release to the public, but we can discuss a bit further if you send me an email (listed on my website).
Delete