Paper Breakdown: A Heuristic Approach to Finding Diverse Short Paths (Caleb Voss et. al.)

A Heuristic Approach to Finding Diverse Short Paths (Caleb Voss, Mark Moll, and Lydia E. Kavraki) is a motion planning paper from Rice University's Kavraki Lab. The paper specifically examines graph-based motion planning, and aims to produce multiple diverse plans from the start to the goal, to make a robotic system robust to changing conditions. In particular, it would be computationally expensive to constantly update the edge weights in a graph if the underlying environment it models were dynamically changing. With the authors' approach, one only needs to check the potential paths for validity. The diversity of the paths makes it more likely that the system will succeed, since an obstacle blocking one path will likely block similar paths.

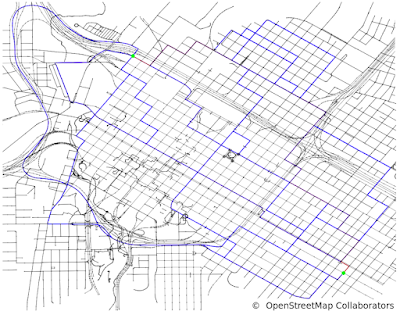20 diverse paths from a start to a goal through downtown Houston, from Fig 6 of the paper.

Background

Graph-based motion planners represent the set of robot configurations as nodes in a graph, where edges indicate it's possible to move between configurations. Edges weights represent the cost of moving between two configurations. Usually, an appropriate distance metric (e.g. Euclidean distance, Manhattan distance) is used to weight edges, but any task-appropriate cost works. For example, the edges in the above graph, representing the roads in downtown Houston, could have a cost depending on distance and speed limit. When a configuration space is continuous, the nodes can only provide an approximation, but the probability of a failure decreases to zero* as the number of nodes is increased. (*There are various technical considerations for when this is true, depending on the algorithm.)

In practice, most of the research effort in graph-based motion planning focuses on the construction of the graph itself, usually from random samples drawn from the configuration space. This is referred to as Sampling-Based Motion Planning. For scenarios where one wants to make many different motion planning queries, the Probabilistic Roadmap (PRM) is perhaps the canonical example.

The idea of producing multiple distinct paths in a graph, which is considered in this paper, leads to several interesting algorithmic and graph-theoretic questions. Researchers have considered the k-shortest path problem, the k-shortest disjoint paths, and so on. These problems appear in varied fields, including (according to Wikipedia) computational linguistics, network routing, and bioinformatics, beyond the obvious path planning examples.

Methodology

The root idea behind this paper is that in motion planning problems, similar paths are likely to fail together. For example, and obstacle that blocks one path may also block nearby paths. And traffic on one street frequently leads to backups on nearby streets as well. Furthermore, paths which share many edges are more likely to fail simultaneously, independent of these domain-specific factors.

In order to describe the diversity of a set of paths, the authors begin with a metric for path similarity. They use the Fréchet distance, restricted to the vertices of a path in the graph. I find that Wikipedia's intuitive definition is quite helpful, and the paper notes that in this discrete case, it can be computed efficiently using dynamic programming. Using the Fréchet distance metric, the authors can then quantify the diversity of a set of paths. They define the "diversity" to be the smallest Fréchet distance between any two paths in the set, and the "robust diversity" to be the sum of the pairwise Fréchet distances (with a normalization factor).

The actual algorithm that puts all their ideas into code is quite clearly presented in the paper. The algorithm begins by computing the shortest path on the graph with no modifications. Then, a branching process begins, where the graph is iteratively modified in various ways, and shortest paths are computed through these modified graphs. In particular, obstacles are added by choosing a random location along the previous optimal path, forcing the new shortest path to choose a significantly different route. The branching comes from trying multiple different places for the obstacle, so different combinations of increasingly many obstacles are considered as the algorithm runs. Hyperparameters allow a developer to tune the size of the obstacles and the number of branches per iteration. The authors include a discussion on how to select the hyperparameters.

Results

The paper includes both theoretical and empirical analysis. The theoretical analysis consists of two theorems. The first theorem guarantees for a small enough obstacle radius, the probability that a single edge gets removed by an obstacle is nonzero. The second theorem uses this fact to prove that, for a sufficiently small obstacle radius, the probability that a given path appears in the diverse set approaches 1 as the number of paths in the set approaches the total number of paths.

It's not clear how applicable these theoretical results are in practice, since it seems that one would want to use a larger obstacle radius than one that just removes a single edge at random. I can see why the single edge-removing obstacle radius is necessary for the proof of Theorem 2, but it would be much more interesting if this could be avoided. It definitely seems like such

As for the empirical performance, it looks really good! The example with the downtown Houston roadmap shown earlier in the blog post is an excellent demonstration in a real-world scenario. In less structured worlds (i.e. where the graph is built by a PRM), the method also shows nice performance. One example was a grid of obstacles, where the robot could pick any continuous path among them. In this case, the set of diverse paths contained many homotopy-distinct paths (i.e. one path could not be continuously deformed into another).

The diverse path set for the world with a grid of obstacles, from Fig. 1 of the paper.

The only method that is compared is the Eppstein algorithm for distinct shortest paths. I would've liked to see a comparison to an edge-disjoint shortest path algorithm, since these force a stronger diversity requirement than just path distinctness. My intuition is that it wouldn't be very different for the downtown Houston roadmap, but I think it might perform better in the grid obstacle world. (Although in the latter case, I still don't expect it to beat the new method in the paper.)

My Ideas

Since reading this paper, I've been thinking about how to apply this method (or a similar method) before the graph has even been constructed. For example, in high dimensional configuration spaces, even the initial PRM construction can be prohibitively expensive. For example, in the paper Motion Planning around Obstacles with Convex Optimization (Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake), the PRM comparison required various user-created tricks to make it work, and it still took a long time to construct. In particular, the PRM was initialized by growing multiple bidirectional rapidly exploring random trees (BiRRTs) to connect various start and goal configurations.

This technique for constructing a PRM leaves much to be desired. In the worst case, if the PRM growth beyond the initial skeleton doesn't add many new paths between a start and goal, a single added obstacle could make the task appear infeasible (even if it just needed another option). Perhaps the technique of adding obstacles along existing paths could be used to generate many distinct (and diverse) BiRRTs between the various nodes, and then these could form the basis of a more robust PRM.