Paper Breakdown: Parallel Transport Unfolding (Max Budninskiy et. al.)

Parallel Transport Unfolding: A Connection-based Manifold Learning Approach (Max Budninskiy, Gloria Yin, Leman Feng, Yiying Tong, and Mathieu Desbrun) is a recent manifold learning paper from the Applied Geometry Lab at Caltech. The paper presents the Parallel Transport Unfolding (PTU) algorithm, which is an extension to the well-known ISOMAP manifold learning algorithm. ISOMAP estimates the pairwise geodesic distances (distance along the manifold) between all of the input points in the high-dimensional ambient space, and produces an embedding in a low-dimensional space that best preserves these distances. Utilizing tools from the field of differential geometry, PTU improves the estimation of these geodesic distances, in turn improving the resulting embedding of the manifold. Additionally, PTU no longer requires that the source data be geodesically convex, which is an important requirement of the ISOMAP algorithm. In this blog post, I'll be summarizing the contents of the paper, and discussing some new ideas this paper has given me.

Many existing manifold learning algorithms (including the popular LLE and Laplacian Eigenmaps) rely on constructing local embeddings of small regions of the manifold, and then stitching these pieces together into a global embedding. Such an approach requires relatively weak assumptions on the structure of the data. But because global information about the dataset is ignored, these approaches are susceptible to noise in the data. ISOMAP, on the other hand is a global method: it attempts to produce a low-dimensional embedding that attempts to preserve all pairwise geodesic distances of the data (near and far). As a result, ISOMAP is highly resilient to data noise.

However, ISOMAP also has an important requirement about the nature of the data manifold. Geodesic distances are not directly available in an arbitrary point set, and a key part of the ISOMAP algorithm is estimating these distances. This is done by constructing a neighborhood graph on the dataset, and solving the all-pairs shortest path problem on that graph. Herein lies the main limitation of ISOMAP: if the data manifold isn't geodesically convex (i.e. the shortest path between two points leaves the domain of the data), then the estimates for geodesic distance will be inaccurate, and thus, ISOMAP will produce a poor quality embedding of the data. Non-convex regions occur frequently in practice, due to voids in the sampling from the manifold, and along curved edges of the sampled regions.

The effect of a hole in the data domain on the embedding produced by ISOMAP (top), compared to the near ideal embedding produced by PTU (bottom).

PTU presents a more robust technique for estimating geodesic distances. The new technique relies on a tool from differential geometry called parallel transport. Parallel transport describes what happens to a tangent vector as it's moved along the manifold. In ordinary Euclidean space, the vector remains unchanged (it is simply translated in that space). But for a curved surface, simply translating the vector may lead to it no longer being tangent to the manifold; in fact, the idea of translating a vector in an ambient space may not even make sense. Parallel transport describes how to perform the equivalent operation, in a manner that is compatible with the curvature of the manifold.

Visualization of parallel transport of a tangent vector along a genus-2 surface.

Of course, parallel transport is a continuous construction on a manifold, so it doesn't immediately lend itself to discrete computational approaches. To solve this problem, the authors use discrete analogs of various differential geometry constructions. At each point sampled from the manifold, the tangent space is represented as an orthonormal frame in the ambient space, and estimated with a singular value decomposition of the local neighborhood. For two adjacent points, the best orthogonal transformation between these orthonormal frames is used as a discrete analog of the parallel transport operator.

With these constructions, one can now estimated geodesic distances along the manifold. Given a sequence of edges that constitute the shortest path (in the neighborhood graph) between two points, each edge is parallel transported onto the previous tangent space, and then appended to the edge in that space. Once all the edges have been unrolled into a single tangent space, the geodesic distance between the start and end point can be directly computed as the Euclidean distance in that tangent space.

PTU uses these new estimates for geodesic distances to produce an embedding using multidimensional scaling, as in the original ISOMAP algorithm. As a result, PTU is able to significantly outperform ISOMAP, as well as various other manifold learning algorithms. Specific results demonstrate PTU's robustness to non-convex domains, irregular sampling, and data noise, all while maintaining the same time complexity as the original ISOMAP algorithm.

The methodology presented in this paper have given me several ideas for future work. I'm primarily inspired by the authors derivation and use of the discrete parallel transport operator.

For example, a key property of parallel transport is that a geodesic results from the path traced by a tangent vector, as it's continuously transported along its own direction. (This is analogous to how an integral curve can be traced through a vector field in an ordinary Euclidean space.) So the discrete parallel transport operator can be used to estimate geodesics along an unknown manifold, represented only by a set of points sampled from that manifold.

This fact can be directly combined with the process for unwrapping edge sequences between two points, in order to construct the Riemannian normal coordinates. For any point on a Riemannian manifold, it is possible to construct a spherical coordinate system about that point, utilizing the exponential map from the tangent space onto the manifold. The construction is analogous to polar and spherical coordinates in ordinary Euclidean space, where radial lines correspond to the paths traced by geodesics on the Riemannian manifold.

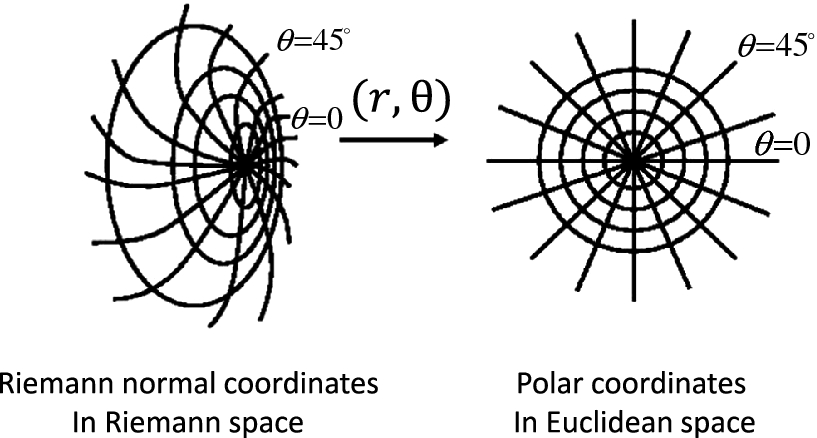(Source)

If every point on the manifold is mapped into the tangent space of a single point, utilizing the discrete parallel transport methodology, this yields an approximation of the Riemannian normal coordinate chart. From this representation of the data, a lot of information can be gleaned. The boundary of this chart (minus the points which lie along the boundary of the manifold) is precisely the cut locus of the center point in the chart. And one can now construct new geodesics emanating from the center point, and examine their behavior on the original manifold. For example, the rate at which geodesics spread is related to the curvature of the manifold via the various comparison theorems of differential geometry, and may even be able to determine the radius of (geodesic) convexity.

I've written some very rough code to experiment with these possibilities, with some early results shown below. The ideas show some early promise, although I'm not likely to continue working on it in the near future.

The estimated Riemannian normal coordinates for points on a sphere (from the perspective of the "north pole"), colored according to their angle of elevation. The black lines are new geodesics, constructed by parallel transporting tangent vectors along their own direction.

The same Riemannian normal coordinate chart as shown above, with points colored by the amount of distortion (computed by how well global pairwise distances are preserved). By only measuring the rate of spread of geodesics, it's possible to estimate the radius of convexity, and bound the size of the neighborhood size to minimize distortion. This has interesting potential for learning atlas representations of manifolds.